Quadrilaterals

In Euclidean plane geometry, a quadrilateral is a polygon with four sides (or edges) and four vertices or corners.http://en.wikipedia.org/wiki/Quadrilateral

Space Figures

Space figures are figures whose points do not all lie in the same plane.

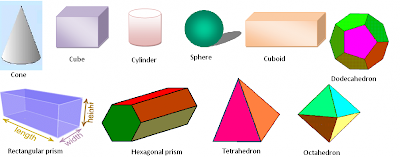
Polyhedrons are space figures with flat surfaces, called faces, which are made of polygons. Prisms and pyramids are examples of polyhedrons.

Cylinders, cones, and spheres are not polyhedrons, because they have curved, not flat, surfaces. A cylinder has two parallel, congruent bases that are circles. A cone has one circular base and a vertex that is not on the base. A sphere is a space figure having all its points an equal distance from the center point.

Circle

A circle is the locus of all points equidistant from a central point.

Definitions Related to Circles

arc: a curved line that is part of the circumference of a circle

chord: a line segment within a circle that touches 2 points on the circle

circumference: the distance around the circle

diameter: the longest distance from one end of a circle to the other

radius: distance from center of circle to any point on it

sector: is like a slice of pie (a circle wedge)

tangent of circle: a line perpendicular to the radius that touches ONLY one point on the circle

origin: the center of the circle

Polygons

A polygon can be defined as a geometric object "consisting of a number of points (called vertices) and an equal number of line segments (called sides), namely a cyclically ordered set of points in a plane, with no three successive points collinear, together with the line segments joining consecutive pairs of the points. In other words, a polygon is closed broken line lying in a plane" (Coxeter and Greitzer 1967, p. 51).

Introduction

Geometry (Ancient Greek: γεωμετρία; geo- "earth", -metron "measurement") is a branch of mathematics concerned with questions of shape, size, relative position of figures, and the properties of space. A mathematician who works in the field of geometry is called a geometer. Geometry arose independently in a number of early cultures as a body of practical knowledge concerning lengths, areas, and volumes, with elements of formal mathematical science emerging in the West as early as Thales (6th Century BC). By the 3rd century BC, geometry was put into an axiomatic form by Euclid, whose treatment—Euclidean geometry—set a standard for many centuries to follow.[1] Archimedes developed ingenious techniques for calculating areas and volumes, in many ways anticipating modern integral calculus. The field of astronomy, especially as it relates to mapping the positions of stars and planets on the celestial sphere and describing the relationship between movements of celestial bodies, served as an important source of geometric problems during the next one and a half millennia. In the classical world, both geometry and astronomy were considered to be part of the Quadrivium, a subset of the seven liberal arts considered essential for a free citizen to master. http://en.wikipedia.org/wiki/Geometry